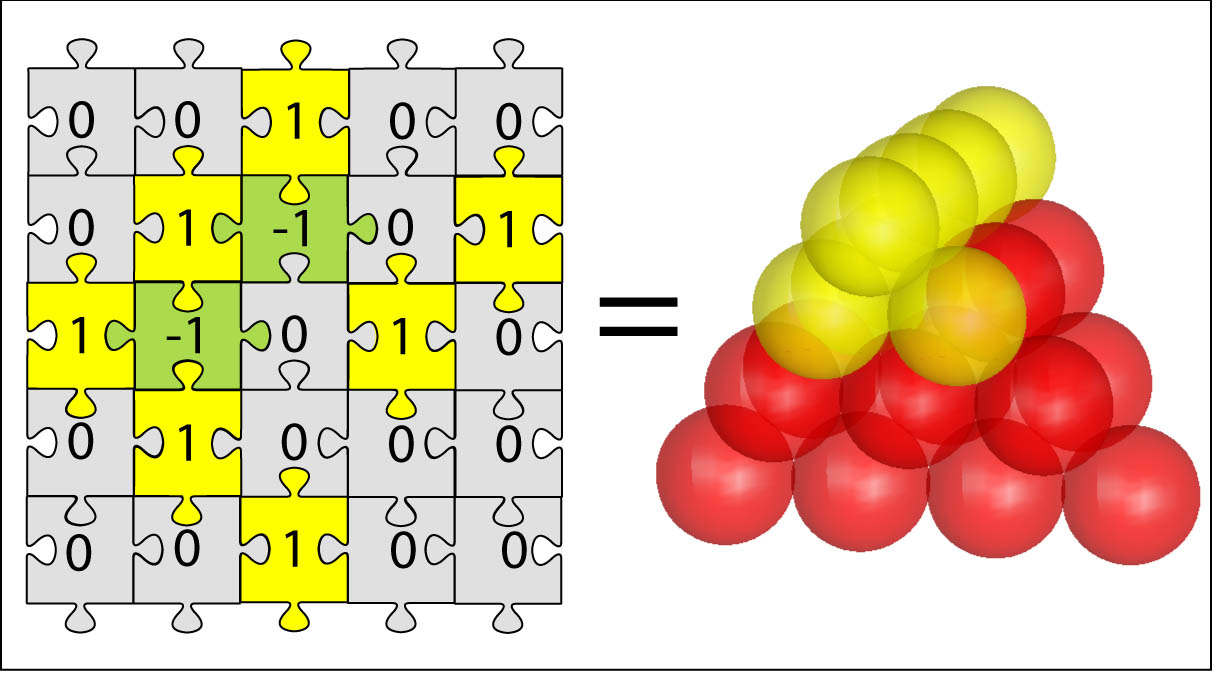
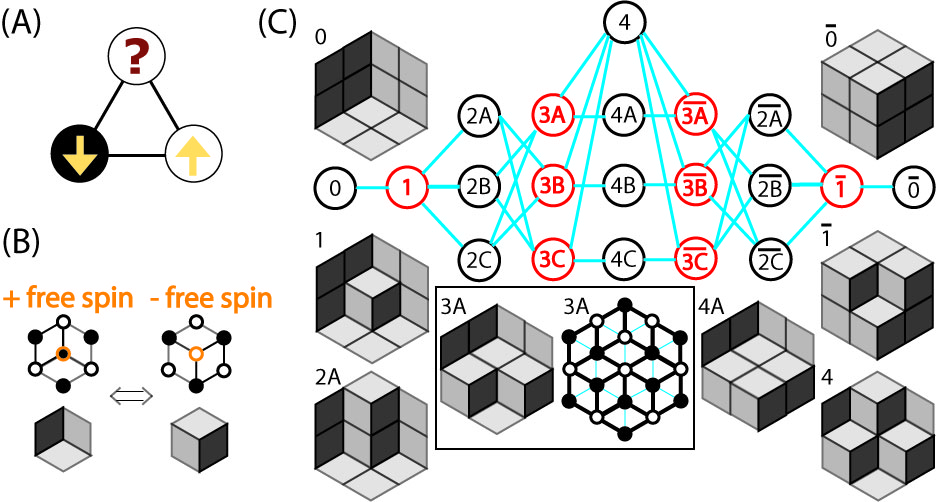
(A): Three antiferromagnetic spins on a triangle cannot simultaneously satisfy all their interactions, i.e. frustration. (B): The central spin has three up and three down neighbors, so that it can flip freely without energy change. Satisfied bonds can be viewed as cubes. The +/- free spin flip corresponds to adding/removing a cube. (C): The 2 x 2 x 2 cube stacks are stable against gravity along the [1,1,1] direction. Stack configurations have one-to-one correspondence to Ising ground states under "hexagon boundary condition", e.g., see configuration 3A. In the right 3A configuration, the black lines are satisfied bonds forming rhombuses and the blue lines are frustrated bonds. In total, there are 20 legal stacks, i.e., 20 nodes in the phase-space network. The network is bipartite, i.e., consisting of alternating red (even number of cubes) and black (odd number of cubes) states.

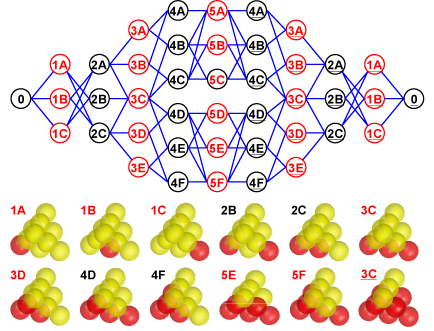
The 42-node phase-space network of the 4x4 spin ice
under the domain-wall boundary condition. The corresponding
sphere stacks of some states are shown in the bottom
panel. 3C denotes the complementary configuration of 3C.

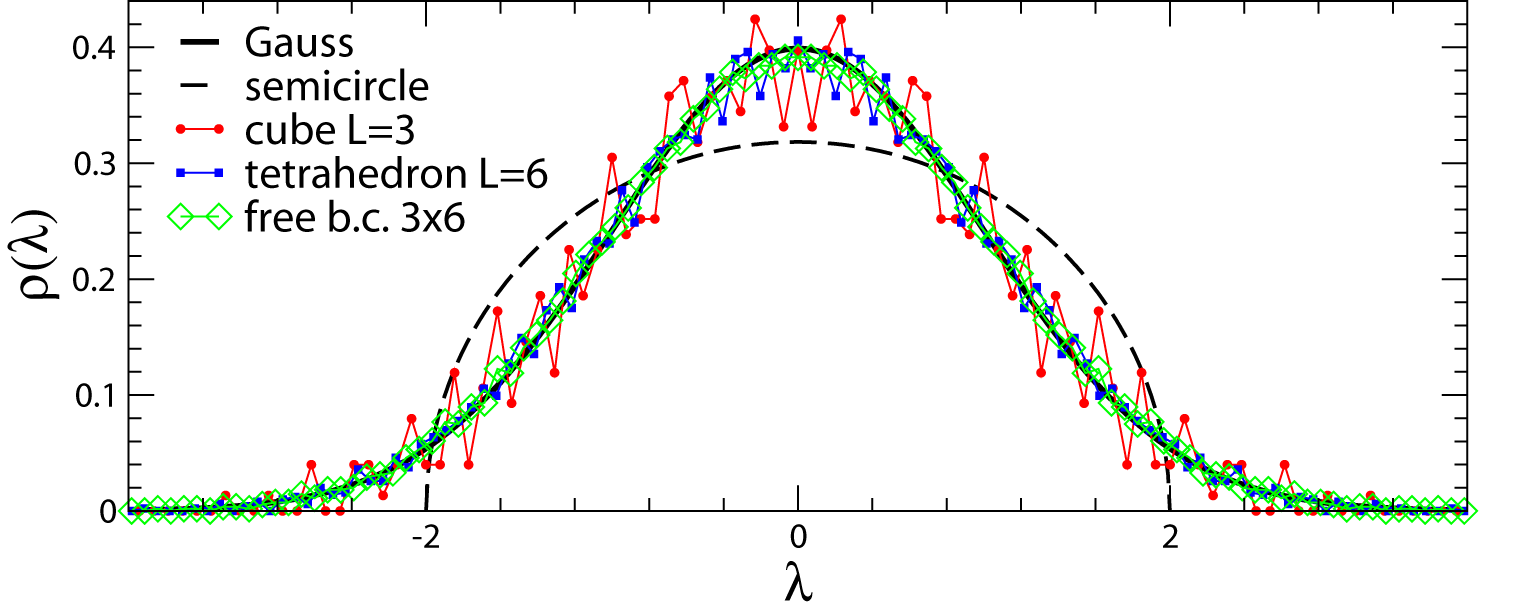
Spectral densities of phase-space networks, i.e. the rescale probability distribution of eigenvalues of the connectivity matrixes of the networks. Variances are rescaled to 1. Different frustrated systems under different boundary conditions exhibit the same Gaussian distribution. This distinguishes phase-space networks from other known networks. The spectral densities exhibit the Wigner's semicircular distribution (dashed curve) for random networks, the triangular distribution of power-law tails for scale-free networks and irregular distributions for other known networks.

Ref: Phase-space networks of geometrically frustrated systems Yilong Han, Phys. Rev. E 80, 051102 (2009)